Prisma
En geometría, un prisma es un poliedro con una base poligonal de n lados, una copia de traslación (no en el mismo plano que la primera), y otras n caras (todas necesariamente deben ser paralelogramos) que une los lados correspondientes de las dos bases. Todas las secciones transversales paralelas a las caras de la base son iguales. Los prismas se nombran para su base, por lo que un prisma de base pentagonal se llama un prisma pentagonal. Los prismas son una subclase de los prismatoides.
VOLUMEN
El volumen de un prisma es el producto del área de la base y la distancia entre las dos caras de base, o la altura (en el caso de un prisma no derecho, tener en cuenta que esto significa la distancia perpendicular).
Por consiguiente, el volumen es:
donde B es el área de la base y h es la altura. Por lo tanto, el volumen de un prisma, cuya base es un polígono regular de n lados con una longitud de lado s, es:

ÁREA DE LOS PRISMAS REGULARES
PRISMA
ÁREA Y VOLUMEN DEL PRISMA
-
PIRÁMIDE
ÁREA Y VOLUMEN DE LA PIRÁMIDE
-
POLIEDROS REGULARES
DEFINICIÓN
Tiene todos sus ángulos diedros y todos sus ángulos poliedros iguales y sus caras son polígonos regulares iguales.Sólo hay cinco poliedros regulares.CLASIFICACIÓN DE POLIEDROS REGULARES:
-
- Su superficie está formada por 4 triángulos equiláteros iguales.Tiene cuatro vértices y seis aristas.Es una pirámide triangular regular.
Área y volumen del tetraedro
Como un tetraedro está formado por 4 triángulos equilaláteros, podemos hallar el área de un triángulo equilátero y multiplicar por 4 para obtener el área del tetraedro.-
- Su superficie está constituida por 6 cuadrados.Tiene 8 vértices y 12 aristas.Es un prisma cuadrangular regular.
Área y volumen del cubo
-
- Su superficie consta de ocho triángulos equiláteros.Tiene 6 vértices y 12 aristas.Se puede considerar formado por la unión, desde sus bases, de dos pirámides cuadrangulares regulares iguales.
Área y volumen del octaedro
Dodecaedro
Área y volumen del dodecaedro
Icosaedro
Área y volumen del icosaedro
característicasSus caras son regiones poligonales congruentes entre si
sus ángulos también son iguales
son convexos
cumplen con el teorema de euler
caras + vértices = aristas + 2
x ejemplo el cubo
6 + 8 = 12 + 2
solo existen 5
Tetraedro
Hexaedro
Octaedro
Dodecaedro
Icosaedro-
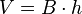










No hay comentarios:
Publicar un comentario